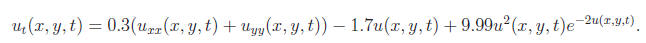Majid Bani-Yaghoub, Ph.D.Professor of Applied Mathematics
Office: Manheim 205
A
|
Numerical Simulations of a Nonlocal Delayed Reaction-Diffusion Model
1. Convergence of PDE solution to stationary wavefront
|
To illustrate the formation and stability of wave solutions we turn our attention to a
class of nonlocal delayed RD equation proposed by So et al (2001, Proc. R. Soc.
Lond. A, 457, 1841–1853). In particular, the
authors adopted Smith-Thieme’s approach to obtain the following model of single
species population.
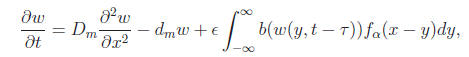
where x ∈ R, 0 < ε≤ 1, w(x, t) represents the total mature population u(x, a, t) at age a, time t and position x that is given by
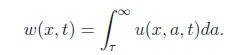
The kernel function is given by
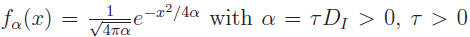
Formation of the traveling waves of the model with constant delay (τ = 12)
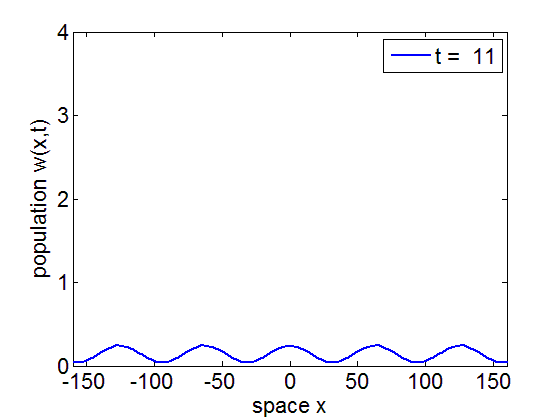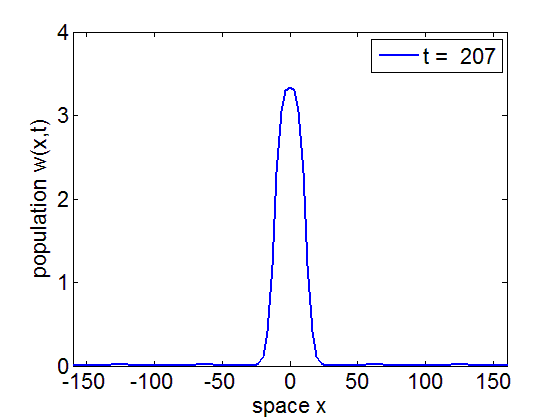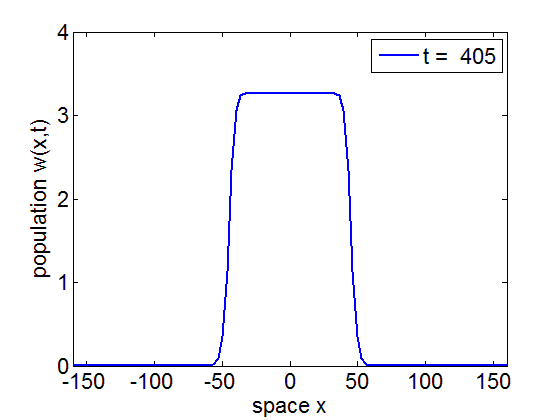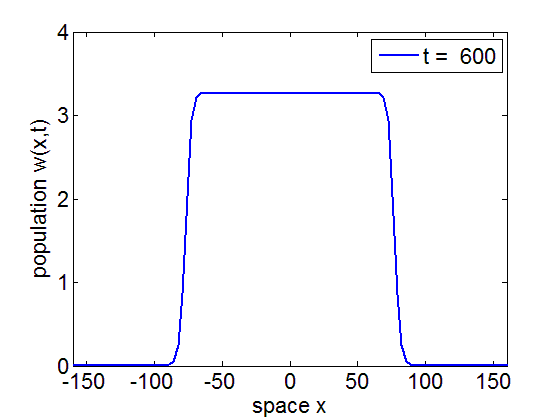
Formation of traveling waves with Gibbs phenomenon due to increasing delay
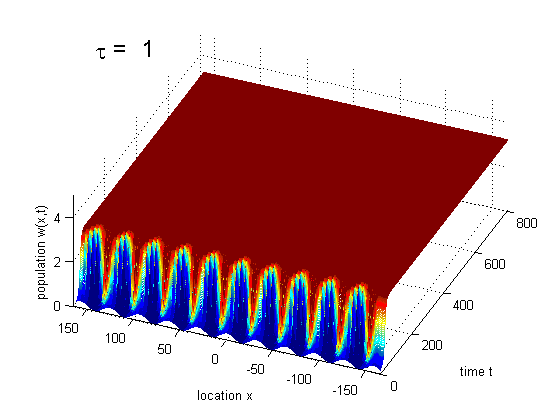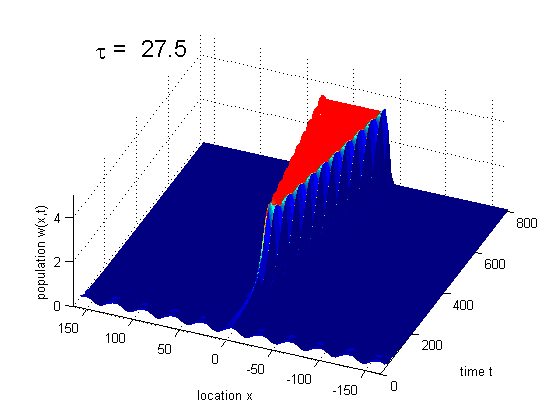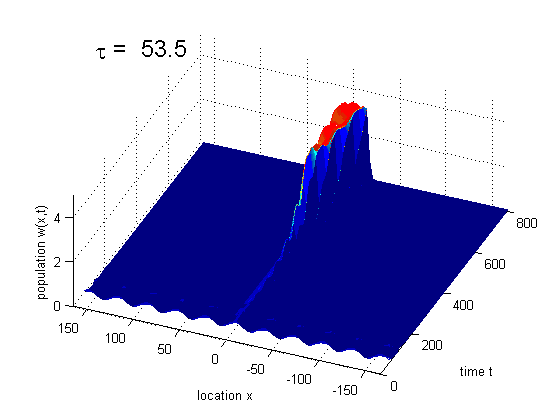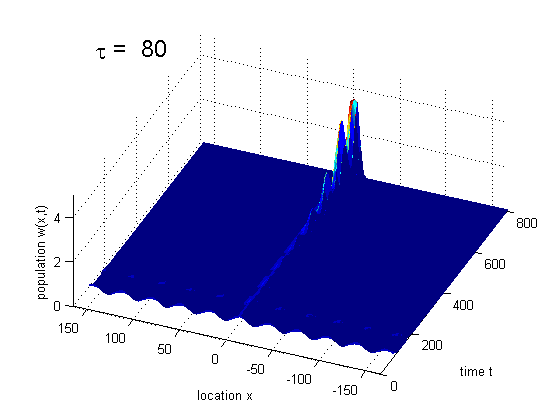
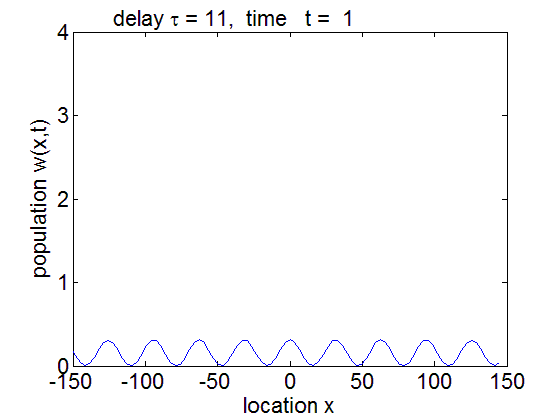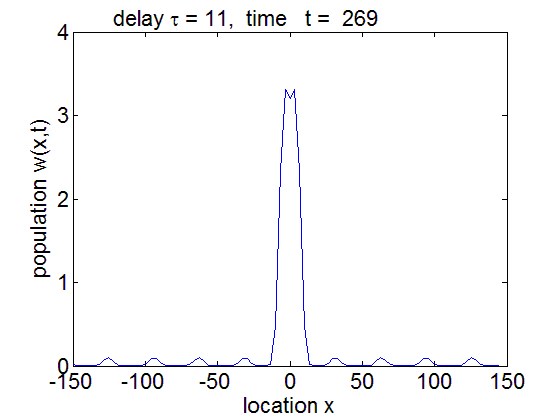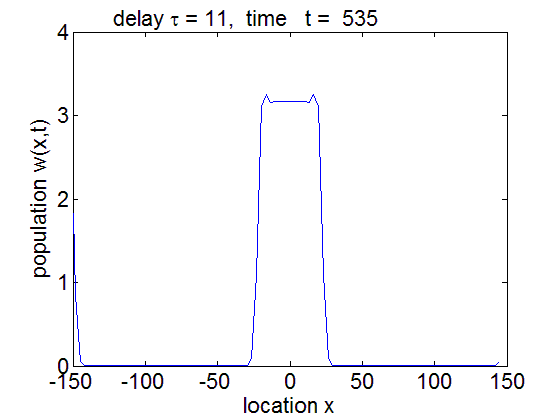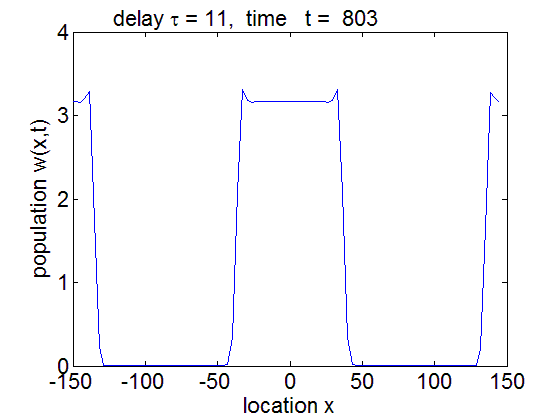
PDE solution for τ = 11
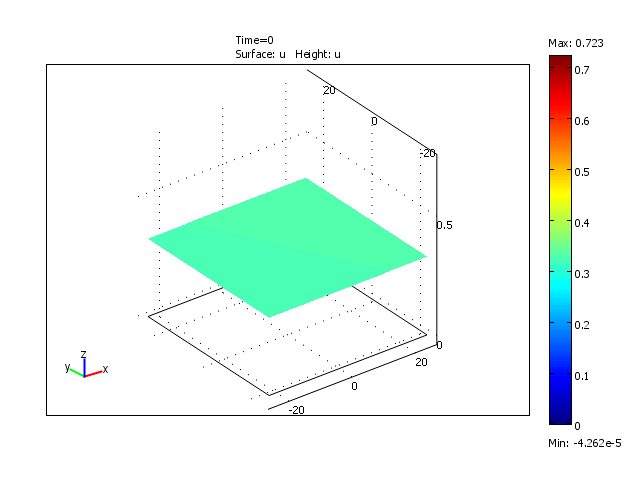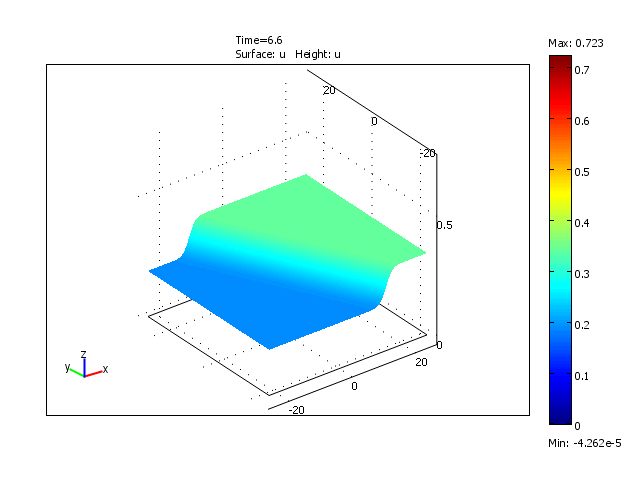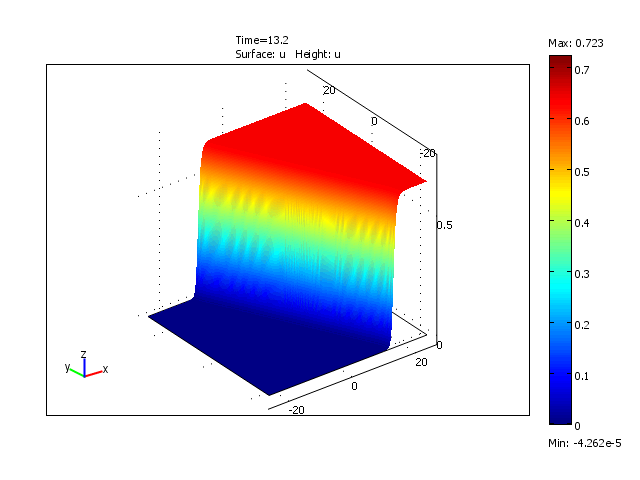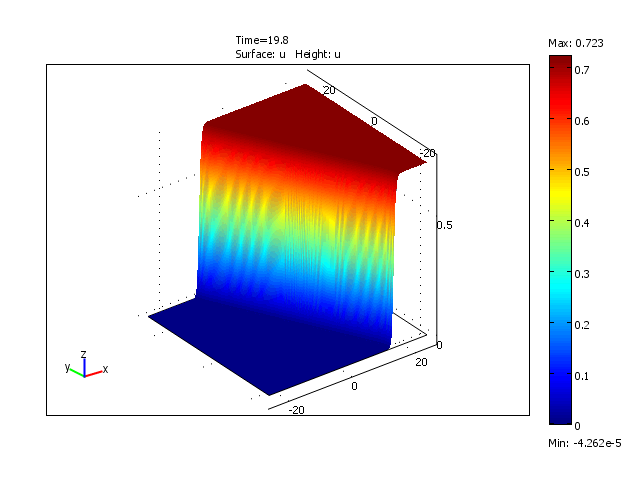
Formation of a wavefront in a 2-dimensional domain for the reduced model
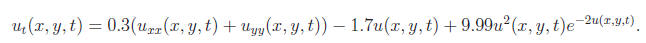
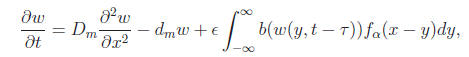
where x ∈ R, 0 < ε≤ 1, w(x, t) represents the total mature population u(x, a, t) at age a, time t and position x that is given by
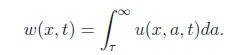
The kernel function is given by
Formation of the traveling waves of the model with constant delay (τ = 12)

Formation of traveling waves with Gibbs phenomenon due to increasing delay

PDE solution for τ = 11

Formation of a wavefront in a 2-dimensional domain for the reduced model