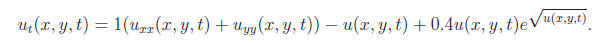Majid Bani-Yaghoub, Ph.D.Professor of Applied Mathematics
Office: Manheim 205 A |
Numerical Simulations of a Nonlocal Delayed Reaction-Diffusion Model
1. Convergence of PDE solution to stationary wavefront
|
To illustrate the formation and stability of wave solutions we turn our attention to a
class of nonlocal delayed RD equation proposed by So et al (2001, Proc. R. Soc.
Lond. A, 457, 1841–1853). In particular, the
authors adopted Smith-Thieme’s approach to obtain the following model of single
species population.
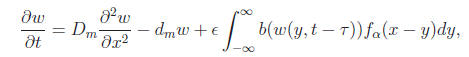
where x ∈ R, 0 < ε≤ 1, w(x, t) represents the total mature population u(x, a, t) at age a, time t and position x that is given by
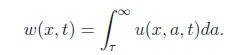
The kernel function is given by
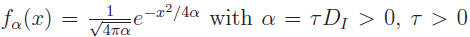
As the immature population becomes immobile (i.e. when α → 0), the kernel function f(x) is changed to Dirac delta function and therefore the model reduces to
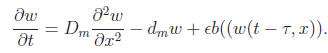
Convergence to Stationary Wavefront
It is numerically shown that the solution of the initial value problem corresponding to the model may converge to the stationary wave front of the model.
blue= PDE Solution
red = Stationary Wavefront
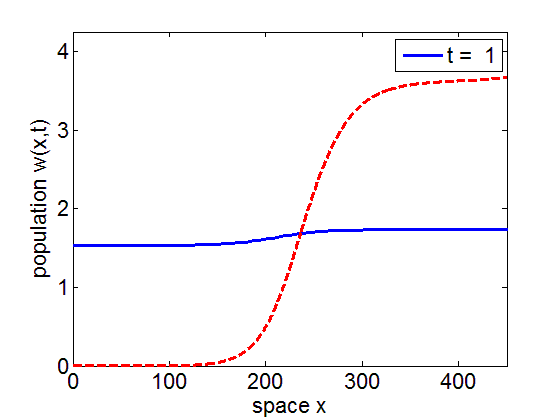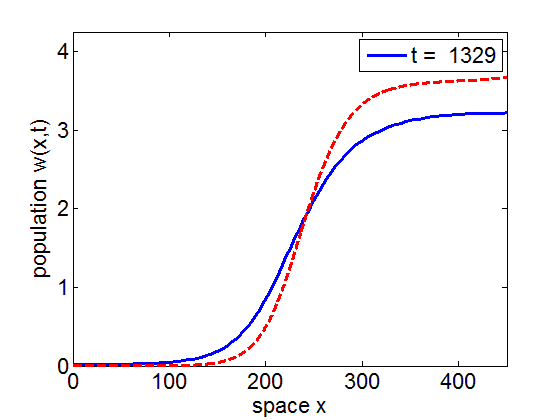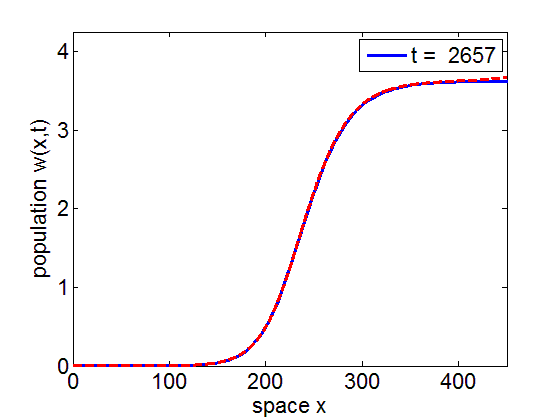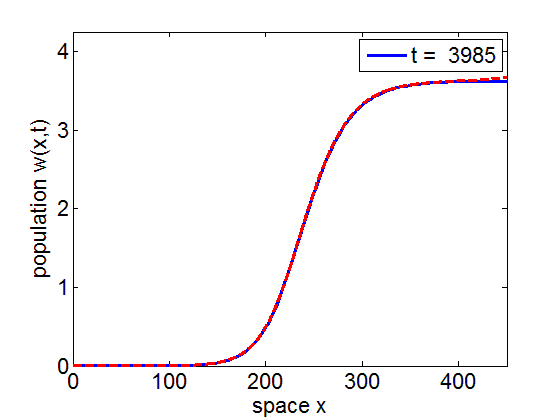
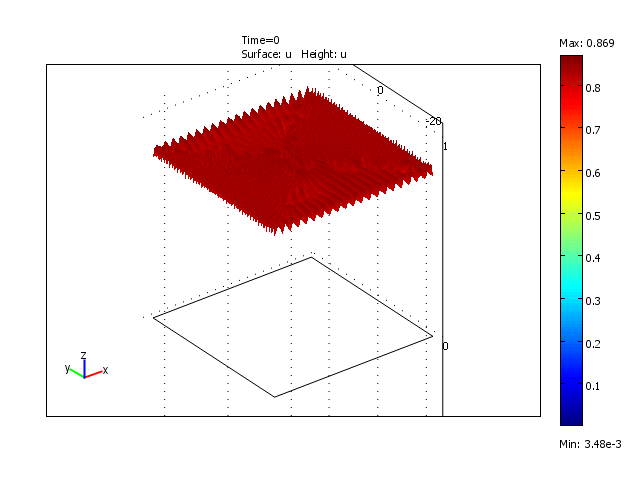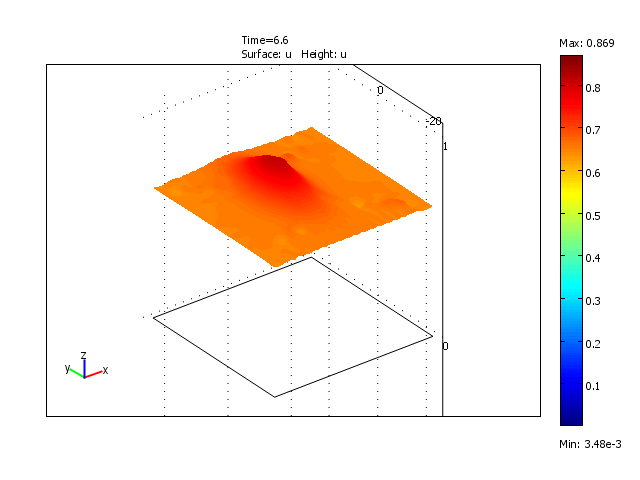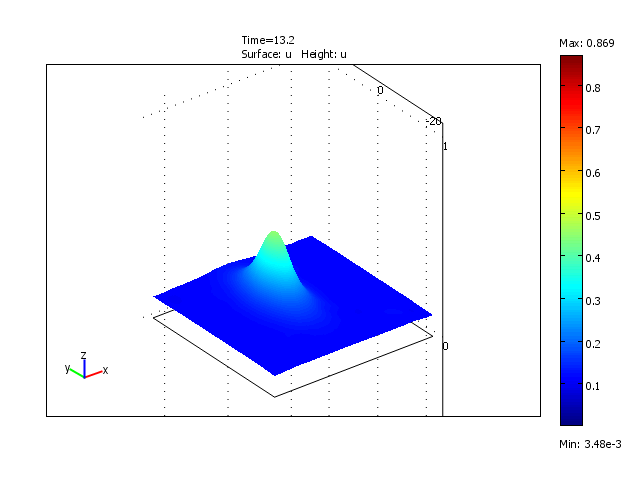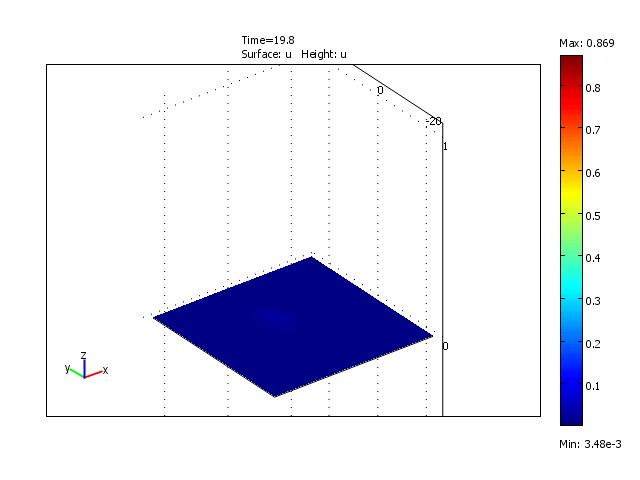
Formation and disappearance of a wave pulse in the 2-dimensional domain for the reduced model
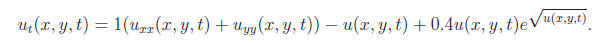
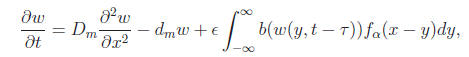
where x ∈ R, 0 < ε≤ 1, w(x, t) represents the total mature population u(x, a, t) at age a, time t and position x that is given by
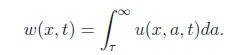
The kernel function is given by
As the immature population becomes immobile (i.e. when α → 0), the kernel function f(x) is changed to Dirac delta function and therefore the model reduces to
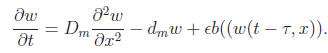
Convergence to Stationary Wavefront
It is numerically shown that the solution of the initial value problem corresponding to the model may converge to the stationary wave front of the model.
blue= PDE Solution
red = Stationary Wavefront

Formation and disappearance of a wave pulse in the 2-dimensional domain for the reduced model