Majid Bani-Yaghoub, Ph.D.

Research Interests

Ordinary, Partial and Delay Differential Equations with applications in Biology, Nonlinear Wave Equations, Modeling and Analysis of Infectious Diseases and Single Species Populations

 

Statement

I am a member of the UMKC Applied Mathematics Group and I welcome interdisciplinary projects leading to grant proposals or peer-reviewed publications. My research includes but not limited to nonlinear analysis of delayed nonlocal reaction–diffusion equations, numerical simulation of traveling and stationary wave solutions, and infectious disease modeling. Below is a brief description of recent research projects.

 

Current Research Projects

 

 

a) Enhancing Mathematical Models to Investigate the Influences of Climate Change on Zoonotic Spillover

 

Most infectious disease outbreaks involve transmission from animals to humans, known as zoonotic spillover. Several studies provide evidence that climate change can influence the frequency and occurrence of zoonotic spillover. Nonetheless, current mathematical models have largely overlooked the effects of climate change on zoonotic spillover. By enhancing the modeling approaches, the researchers of this multidisciplinary project seek to understand what challenges zoonotic pathogens must overcome to transmit from wild animal hosts to humans or other animals, how climate change can reduce these challenges and make it more plausible for zoonotic pathogens to live within and between new species, and what kinds of environments have a higher likelihood of zoonotic spillover in the view of climate change.

The research team will use decades of weather, wildlife population, and zoonotic disease data to identify significant variables that can be incorporated into the models and to accurately estimate epidemiological predictors of spillover (e.g., the force, speed, and direction of disease spread and the basic reproduction number) as functions of significant weather and environmental factors. The numerical simulations of the calibrated models will help the researchers elucidate the underlying mechanisms governing the ecology of zoonotic disease and predict possible influences of climate change. Furthermore, this study builds on the existing wave theory of pathogen and population dispersal to advance the theoretical knowledge of traveling and stationary waves, including their existence, uniqueness, stability, and asymptotic behaviors. The analytical and computational tools, template codes, and tutorials for enhanced modeling and simulating zoonotic spillover will be released on a GitHub page dedicated to this project.

 

b) Antimicrobial Resistance: A One Health Perspective

Antimicrobial Resistant (AMR) pathogens have become a significant public health threat. By developing and implementing novel mathematical and computation models, the long-term goals are to optimize AMR control and preventive interventions and to improve the health equity. The central hypothesis is that the outputs of mathematical and computation models will provide optimized and effective guidelines to reduce the threat of AMR pathogen spread and reduce health disparities in healthcare settings. The rationale underlying this project is to fill the critical gap in modeling workforce capacity and develop a new generation of mathematical models for healthcare research. The central hypothesis will be tested by pursuing three specific aims to develop and employ a, (i) One Health modeling approach to understand the source, distribution and spread of AMR Enterobacteriaceae with a focus on Extended-spectrum beta-lactamase (ESBL)-producing E. coli, (ii) a novel Real-Time modeling approach to identify AMR pathogen transmission by asymptomatic spreaders and contaminated medical devices in hospitals, (iii) a novel Agent-Based Nested modeling approach to identify the effects of caregivers as vectors of disease spread, and effects of limited staffing and specialized care on equitable quality of care in nursing homes. We will pursue these aims using an innovative combination of mathematical and computational modeling techniques. These include both recently developed techniques of including human behavior in models and more-established techniques that have been applied very little to the study of health equity and AMR pathogen spread. The workforce development objectives of this proposal are to (i) enhance mathematical and computational modeling research capabilities of the public health workforce and (ii) increase the number of junior modeling professionals that are trained and experienced in modeling transmission of pathogens in healthcare settings partly incorporated with health disparities.

 

Completed Research Projects

 

 

a) Epidemic Waves of COVID-19

 Focusing on Kansas City MO COVID-19 data, we have been modeling and analyzing the spatial and temporal patterns of COVID-19 since the beginning of the pandemic.

 

Published Articles  

• AlQadi, H., Bani-Yaghoub, M. (2022) Incorporating global dynamics to improve the accuracy of disease models: Example of a COVID-19 SIR model, PloS one 17.4 https://doi.org/10.1371/journal.pone.0265815

•  Alqadi, H., Bani Yaghoub, M., Wu, S., Francisco, A., Balakumar, S. (2022) Prospective Spatial-Temporal Clusters of COVID-19 in Local Communities: Case Study of Kansas City, Missouri, United States. Epidemiol Infect https://doi.org/10.1017/S0950268822000462

•  AlQadi, H., Bani-Yaghoub, M., Balakumar, S., Wu, S., Francisco, A. (2021) Assessment of Retrospective COVID-19 Spatial Clusters with Respect to Demographic Factors: Case Study of Kansas City, Missouri, United States. International Journal of Environmental Research and Public Health 18, no. 21: 11496  https://doi.org/10.3390/ijerph182111496

b) Efficacy of Interventions Affected by Antimicrobial Resistance

We recalculated the effectiveness of environmental decontamination and antimicrobial drug administration by including pathogen trait evolution in the models of disease transmission between the hosts. In addition, we proposed a new methodology to analyze the impacts of host and pathogen dispersal on coinfection dynamics using the example of Escherichia coli O157:H7. A multi-strain Susceptible–Infected–Susceptible model was extended to a Reaction–Diffusion coinfection model of E. coli O157:H7 transmission, which includes intermittent shedding and pathogen growth in the environment. The significance of this study lies in utilizing the nonlinear wave theory to analyze effects of antimicrobial resistance on dynamics of coinfection with respect to host movements and pathogen transport. 

 

Published Articles  

• Bani-Yaghoub, M., Wang, X., Aly, S. (2022) Spatio-temporal analysis of coinfection using wavefronts of Escherichia coli O157:H7 in a dairy cattle farm, Journal of Computational and Applied Mathematics 406 https://doi.org/10.1016/j.cam.2021.113936

•  Bani-Yaghoub, M., Wang, X., Pithua, P., Aly, S. (2019) Effectiveness of control and preventive measures influenced by pathogen trait evolution: Example of Escherichia coli O157:H7, Journal of Computational and Applied Mathematics, 362, 366-382 https://doi.org/10.1016/j.cam.2018.09.008

 

c) Nonlinear Waves Delayed Population Models

To illustrate the formation and stability of wave solutions we turn our attention to a class of nonlocal delayed RD equation proposed by So et al (2001, Proc. R. Soc. Lond. A, 457, 1841–1853).  In particular, the authors adopted Smith-Thieme’s approach to obtain the following model of single species population.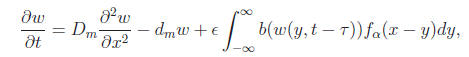

where x ∈ R, 0 < ε≤ 1, w(x, t) represents the total mature population u(x, a, t) at age a, time t and position x that is given by

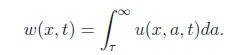
The kernel function is given by



As the immature population becomes immobile (i.e. when α → 0), the kernel function f(x) is changed to Dirac delta function and therefore the model reduces to




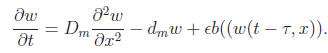
Convergence to Stationary Wave Pulse

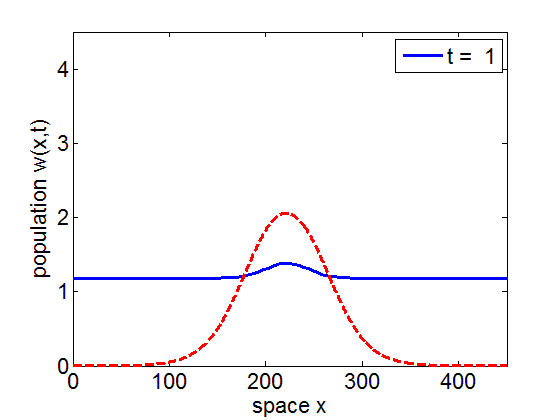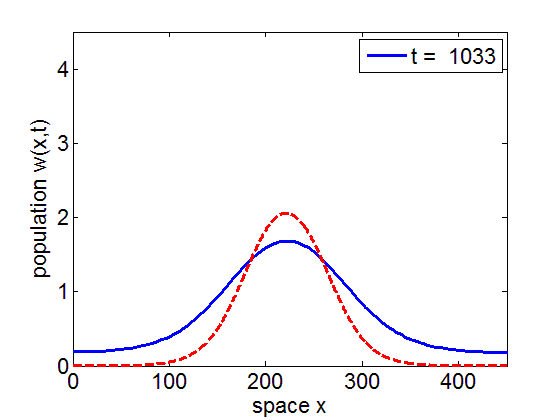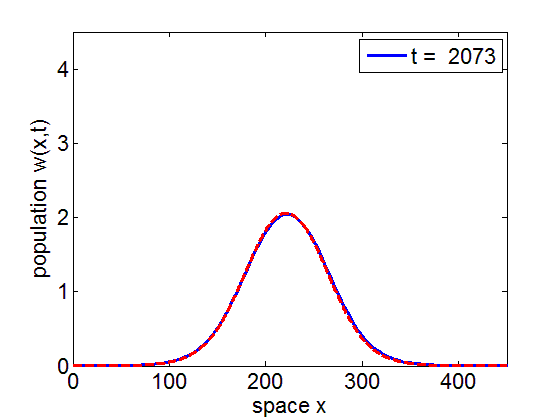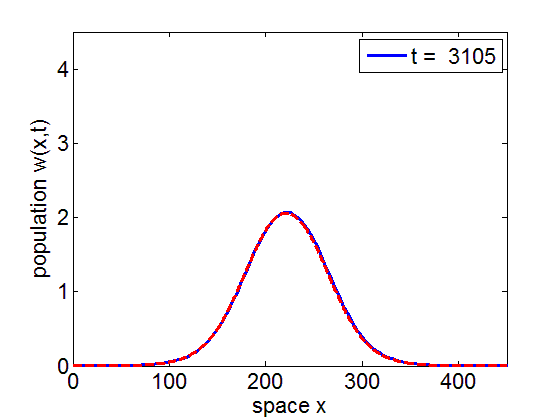
It can be numerically shown that the solution of the initial value problem corresponding to the model may remain in a neighborhood of the stationary pulse and fronts of the reduced model for long periods of time.


blue= PDE Solution
red = Stationary Wave Pulse

More Simulations

1. Convergence of PDE solution to stationary wavefront

2. Impacts of the maturation time delay on PDE solution

3. Impacts of the diffusion rates on wave solutions

4. Formation of traveling wave solutions

§  Main collaborator: Dr. Guangming Yao  gyao@clarkson.edu, Department of Mathematics, Clarkson University

§  Funding: CAS Startup Fund (Partial), 2012-2015, Internal Travel Grant

 

§  Published articles:

1.  Bani-Yaghoub, M., Ou, C., Yao, G. (2019) Delay-induced instabilities of stationary solutions in a single species nonlocal hyperbolic-parabolic population model, Discrete and Continuous Dynamical Systems, Series S
2. Bani-Yaghoub, M. (2018) Numerical simulations of traveling and stationary wave solutions arising from reaction-diffusion population models with delay and nonlocality, International Journal of Applied and Computational Mathematics 4 (1), 28 
3. Bani-Yaghoub, M. (2017) Introduction to Delay Models and Their Wave Solutions, arXiv:1701.04703, 1-20
4.  Bani-Yaghoub, M. (2016) Approximate Wave Solutions of Delay Diffusive Models Using a Differential Transform Method, Applied Mathematics E-Notes 16, 99-104
5.  Bani-Yaghoub, M., Yao, G., Voulov, H. (2016) Existence and stability of stationary waves of a population model with strong Allee effect, Journal of Computational and Applied Mathematics 307, 385–393, doi:10.1016/j.cam.2015.11.021
6.  Bani-Yaghoub, M. (2015) Approximating the traveling wavefront for a nonlocal delayed reaction-diffusion equation, Journal of Applied Mathematics and Computing, 1-18, 10.1007/s12190-015-0958-7
7. Bani-Yaghoub, M., Amundsen, D.E. (2015) Oscillatory traveling waves for a population diffusion model with two age classes and nonlocality induced by maturation delay, Computational and Applied Mathematics, 34 (1), 309-324
8. Bani-Yaghoub, M., Yao, G., Reed, A., (2014) Modeling and Numerical Simulations of Single Species Dispersal in Symmetrical Domains, International Journal of Applied Mathematics 27 (6): 525-547

 

d) Livestock Disease Modeling: Johne's Disease & E. Coli

Johne’s disease (JD) is an incurable and fatal contagious disease of ruminants which is responsible for considerable economic losses in the dairy industry. Cow movements between pens is one of the daily practices in dairy farm management however the impacts of cow movements on the spread of JD have been poorly elaborated. The purpose of this research is to investigate the potential impacts of cattle movement between pens on the dynamics of JD by applying a mathematical modeling approach to the available data.

§  Collaborators: (1) Dr. Patrick Pithua VA-MD College of Veterinary Medicine, Virginia Tech, (2) Dr. Sharif Aly Veterinary Medicine Teaching and Research Center, University of California, Davis, and (3) Dr. Xueying Wang, Department of Mathematics, Washington State University

§  Funding: NA

§  Published article:

 

1. Bani-Yaghoub, M., Wang, X., Pithua, P., Aly, S. (2019) Effectiveness of control and preventive measures influenced by pathogen trait evolution: Example of Escherichia coli O157:H7, Journal of Computational and Applied Mathematics, 362, 366-382

2. Konboon M., Bani-Yaghoub M., Pithua P., Rhee N., Aly S. (2018) A nested compartmental model to assess the efficacy of paratuberculosis control measures on U.S. dairy farms. PLoS ONE 13 (10): e0203190.

3. Bani-Yaghoub, M., Wang, X., Pithua, P., Aly, S. (2018) Effectiveness of control and preventive measures influenced by pathogen trait evolution: Example of Escherichia coli O157:H7, Journal of Computational and Applied Mathematics

e) Wildlife Disease Modeling: Hemorrhagic Disease

Epizootic hemorrhagic disease (EHD) is an often fatal hemorrhagic disease of white-tailed deer and other wild and domestic ruminants. The organism responsible for EHD is Orbivirus, a vector-borne pathogen. The virus requires an insect vector, Culicoides variipennis, and the biting midge, to reach its host, the white - tailed deer. The disease poses a serious threat to white-tailed deer and we need a better understanding of the dynamics of HD transmission in order to be able to control it. The goals of this project are to employ a mathematical modeling approach to analyze the dynamics of EHD transmission, to assess the effectiveness of current control measures, and to provide guidelines that can effectively reduce the prevalence of EHD in the white-tailed deer populations.

 

§  Published articles:

1. Baygents, G., Bani-Yaghoub, M. (2018) Cluster analysis of hemorrhagic disease in Missouri’s white-tailed deer population: 1980-2013, BMC ecology 18 (1), 35
2. Baygents, G., Bani-Yaghoub, M. (2017) A Mathematical Model to Analyze Spread of Hemorrhagic Disease in White-Tailed Deer Population Journal of Applied Mathematics and Physics 5 (11), 2262

 

 

f) Social Network Analysis of Rodents

Measuring long term changes in the social networks of interacting species can reveal vital information about the ecology and evolution of wildlife communities. Although social network analysis is a promising tool to study the structure and dynamics of wildlife communities, the current methods require costly and detailed network data, which often are not available over long time periods (e.g. decades). The present work aims to resolve this issue by developing a new methodology that requires much less detailed data and relies on well-known mathematical Lotka-Volterra (LV) models to quantify the long term changes in the population interactions (e.g. long-term temporal changes from cooperative behavior to competitive behavior).

 

To examine the robustness of this new method, the annual LV models will be selected and specified using the available long-term abundance data (1973- 2003) of Kansas rodents. If successful, the developed methodology can elucidate the presence, quantify the magnitudes, and detect the variability of interactions within and among the rodent species. We also are aware of many other long-term data of the same nature that can be used to analyze the ecology and evolution of population interactions among species other than rodents. Combining the theory and the available data, our long-term goals are (1) to extend the methodology to measure the spatio-temporal changes in the social networks of species residing in the same geographical environment; and (2) to develop a framework to study the possible impacts of climate change on population interactions.

 

 

In the Reaction-Diffusion LV, let y_i (x, y, t)   denote the proportional density of species i at location (x, y) and time t. Specifically, for i =1, ..., 5 y_i (x, y, t)  denotes the proportional density of Cotton Rat (Sigmodon hispidus), Prairie Vole (Microtus ochrogaster), White-footed Mouse (Peromyscus lecuopus), Deer Mouse (Peromyscus maniculatus), and Western Harvest Mouse (Reithrodontomys megalotis), respectively.

 

The following animations represent the the numerical simulations of the Reaction-Diffusion LV model for the years 1976-1979. Using the estimated annual parameter values it can bee seen that the solutions converge to constant equilibrium (y₁, y₂, y₃, y₄, y₅) = (0.415, 0, 0, 0, 0.485 ) around day 1780 (April, 1978) and constant equilibrium (y₁, y₂, y₃, y₄, y₅) = (1, 0, 0, 0, 0 ) around day 2330 (October, 1979).

 

Spatio-temporal dynamics of Prairie Vole is shown below

 

See also

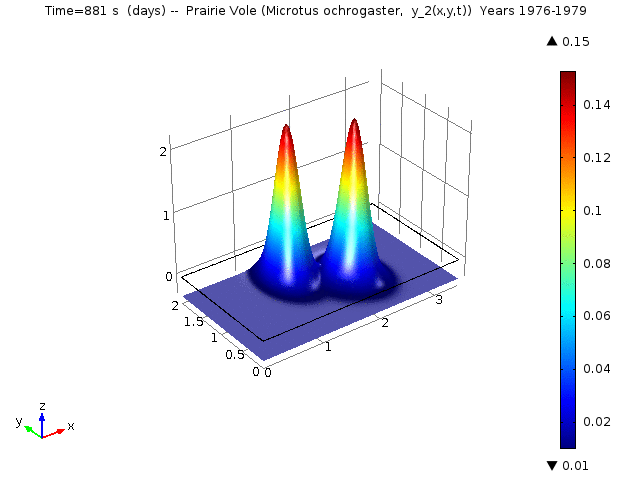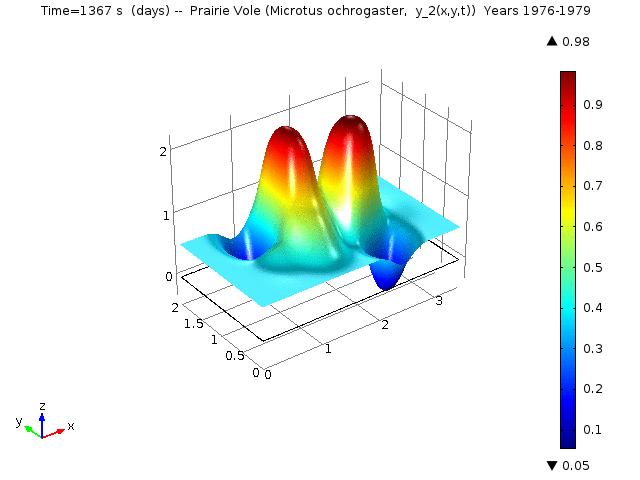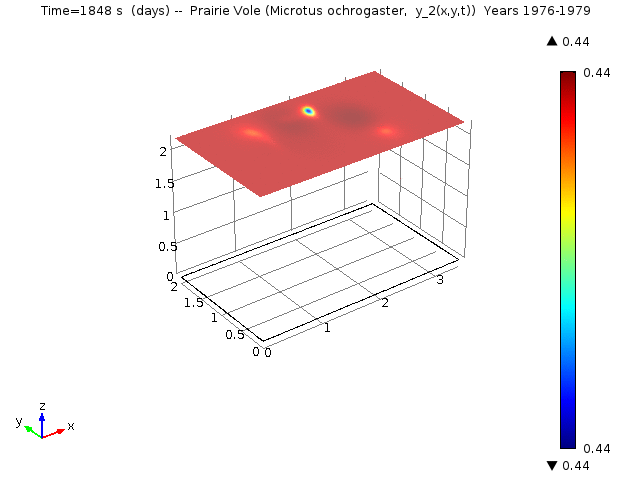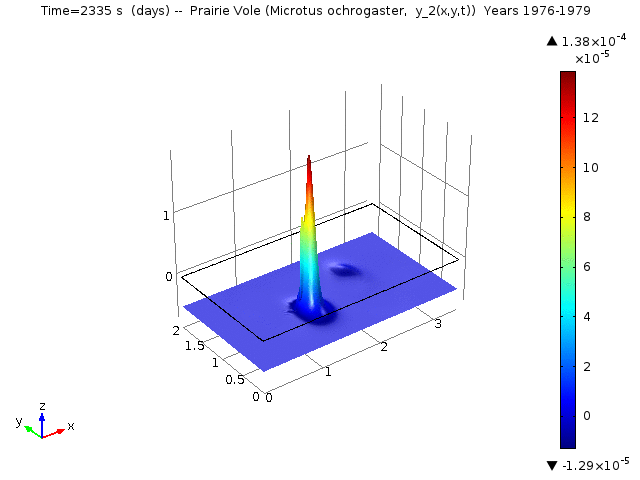
Spatio-temporal dynamics of Cotton Rat

Spatio-temporal dynamics of White-footed Mouse

Spatio-temporal dynamics of Deer Mouse

Spatio-temporal dynamics of Western-harvest Mouse
 

 

§  Collaborator: Dr. Aaron W. Reed reedaw@umkc.edu, UMKC School of Biological Sciences

§  Funding: UMRB, 2015-2016

§ Published articles:  

1.  Bani-Yaghoub, M., Reed, A., (2018) A methodology to quantify the long-term changes in social networks of competing species, Ecological Modeling, 368, 147-157
2. Bani-Yaghoub, M., Reed, A., (2016) Social Network Analysis of a Grassland Rodent Community Using a Lotka-Volterra Modeling Approach, arXiv:1601.01935, 1-3

 

g) Assessment of Smoking Cessation Methods

Using the available data and Markov Chain modeling we assess the interventions motivational interviewing, health education and brief advice in population of smokers who are not ready to quit.

 

§  Collaborator: Dr. Delwyn Catley catleyd@umkc.edu, UMKC Department of Psychology

§  Funding: NA

 § Published articles:

 

Bani-Yaghoub, M., Elhomani, A., Catley, D. (2018) Effectiveness of Motivational Interviewing, Health Education and Brief Advice in a Population of Smokers Who Are Not Ready to Quit. BMC Medical Research Methodology, 18 (1), 52 doi.org/10.1186/s12874-018-0511-0

 

h) Optimal Control of Gang Violence

Using the available data and a time series modeling approach we assess the effectiveness of control measures to reduce the aggravated gun violence and homicide.

 

§  Collaborators: Dr. Andrew M. Fox foxan@umkc.edu and Dr. Kenneth Novak NovakK@umkc.edu, UMKC Department of Criminal Justice & Criminology

§  Funding: CJC 2015-2016

§  Published article:

1. Fox, AM., Novak, KJ., and Bani-Yaghoub, M. (2015) Measuring the Impact of Kansas City’s No Violence Alliance. Kansas City, MO: Department of Criminal Justice and Criminology, University of Missouri-Kansas City, 1-27